머신러닝/딥러닝을 공부하다보면
likelihood라는 단어가 자주 등장한다
이것이 무엇이며, 왜 사용하고, 어떻게 사용하는지 알아보자
Probability
확률 (Probability) : PDF의면적;
확률분포가 고정된 상태에서 해당 관측값(데이터)이 나올 확률, P ( data | distribution )
확률밀도함수 (Probability Density Function, PDF) :연속확률변수의 분포를 나타내는 함수
'확률' 이라고하면 이산 확률을 먼저 떠올리기 쉽다 (동전에서 앞면이 나올 확률? 주사위에서 6이 나올 확률?)
그렇다면 연속 확률은 어떻게 구할까 (고양이의 무게가 4kg 이상 5kg 미만일 확률?)

$$ P(4 \le Cat\ weight < 5\ |\ N(4, 0.5) = 0.477 ) $$
평균이 4이고, 표준편차가 0.5인 정규분포에서
고양이 몸무게가 4kg에서 5kg 사이일 확률은 0.477
무작위로 고양이 한 마리를 선택했을 때 고양이 몸무게가 4kg~5kg일 확률이 47.7%라는 뜻
Likelihood
가능도, 우도 (Likelihood) : PDF의y값;
고정된 관측값(데이터)이 해당 확률분포에서 나왔을 가능성, L ( distribution | data )
그렇다면 Likelihood는 무엇일까?
고양이의 몸무게가 5kg일 때, Likelihood는?

$$ L(N(4, 0.5)\ |\ Cat\ weight = 5) = 0.108 $$
Likelihood는 확률밀도함수 PDF의 y값에 해당하므로 0.108
이번에는 확률밀도함수를 오른쪽으로 조금 움직여서
평균이 5이고, 표준편차가 0.5인 정규분포에서 Likelihood는?

$$ L(N(5, 0.5)\ |\ Cat\ weight = 5) = 0.7979 $$
고양이 무게가 5kg일 때, 평균이 4(위)인 분포보다 평균이 5(아래)인 분포가 데이터를 더 잘 설명한다
"위의 분포보다 아래의 분포에서 주어진 데이터를 더 잘 설명한다, 발생가능성이 높다"
어떤 데이터가 주어졌을 때, 해당 데이터를 잘 설명할 수 있는 분포를 만드는 것
이것이 바로 머신러닝/딥러닝의 목표
머신러닝/딥러닝에서의 Likelihood
MNIST 이미지 데이터 중 하나가 주어지고, 이를 텐서로 표현하면 다음과 같다

그리고 해당 데이터의 Label(정답)은 1이다
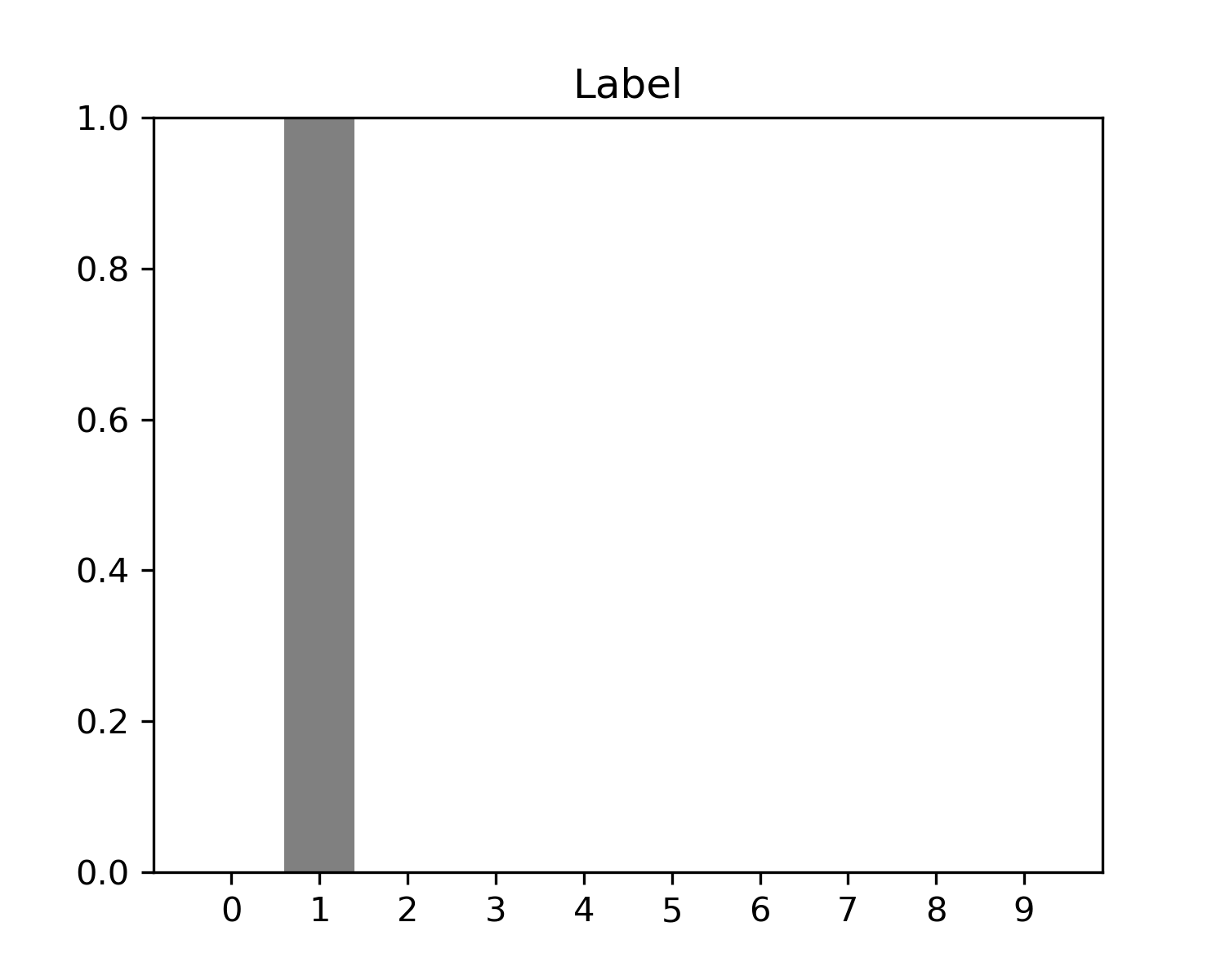
3개의 모델을 구현하여, 모델의 마지막 Softmax layer에서 확률값을 뽑아보면

3개의 모델 중 가장 정답에 가까운 분포는 Model C이다
Model C가 데이터를 가장 잘 설명하는 distribution이라고 할 수 있다
즉, Model C가 Likelihood가 가장 높은 분포이다
데이터를 가장 잘 설명해줄 수 있는 분포를 찾아나가는 것이 머신러닝/딥러닝에서 하는 일!
따라서 우리는 이 Likelihood를 최대화시켜야 한다 → MLE
최대가능도추정, 최대우도추정 (Maximum Likelihood Estimation, MLE) :
각 데이터에 대한 총 가능도(모든 가능도의 곱)가 최대가 되도록 하는 분포를 찾는 것
즉, 데이터를 가장 잘 설명할 수 있는 분포를 찾는 것
동시에 A같은 모델을 C로 만들기 위해 학습을 진행한다 이 때 사용되는 loss → Cross Entropy
Entropy와 Cross Entropy
Entropy
엔트로피를 정확하게 정의하기는 어렵지만
정보 이론에서는 엔트로피를 불확실성의 개념으로 접근할 수 있다
어떤 일의 발생 확률이 낮을수록 정보를 많이 포함하고 있으며, 불확실성이 높고, 엔트로피가 높다고 표현할 수 있다
정보 엔트로피는 다음과 같다
$$ H(q) = - \sum_{i} p(x_i)\log_e p(x_i) $$
동전 던지기와 주사위 던지기를 비교해보면
$$ H(x) = -\left( \frac{1}{2}\ln\frac{1}{2} + \frac{1}{2}\ln\frac{1}{2} = 0.693 \right) $$
$$ H(x) = -\left( \frac{1}{6}\ln\frac{1}{6} + \frac{1}{6}\ln\frac{1}{6} + \frac{1}{6}\ln\frac{1}{6} + \frac{1}{6}\ln\frac{1}{6} + \frac{1}{6}\ln\frac{1}{6} + \frac{1}{6}\ln\frac{1}{6} = 1.792 \right) $$
주사위 던지기의 엔트로피가 더 크다
즉, 주사위 던지기가 동전 던지기보다 더 예측이 어려운 것이라고 볼 수 있다
Cross Entropy
엔트로피에 대한 수식이 다음과 같다면
$$ H(q) = - \sum_{i} p(x_i)\log_e p(x_i) $$
크로스 엔트로피에 대한 수식은 다음과 같다
$$ H_p(q) = -\sum_{i} q(x_i)\log_e p(x_i) $$
크로스 엔트로피는 기존의 엔트로피 수식의 $p(x_i)$가 $q(x_i)$로 바뀐 것
$q(x_i)$는 실제 세상의 확률
$p(x_i)$는 모델을 통해 구한 확률
위에서의 MNIST 예시를 들어 설명해보면

Softmax를 지나서 확률값으로 나온 Model A의 예측 결과가 $p(x_i)$
One-hot encoding으로 이루어진 Label이 $q(x_i)$
사실상 Label이 One-hot encoding이기 때문에
정답을 제외한 나머지는 모두 0이고
정답이 1일 확률에만 로그를 취해 마이너스를 붙이면 Loss가 나온다
Model A는 정답이 1일 확률을 0.05라고 예측했기 때문에 Loss는 다음과 같다
$$ Cross\ Entropy\ Loss = -\log_e (0.05 + 1e-7) = 2.996 $$
뒤에 $1e-7$을 더해주는 이유?
로그에 0이 오게되면 무한대가 될 수 있기 때문에 아주 작은 수를 추가해주는 것
그렇다면 위에서 예시로 들었던
Model A, B, C 각각의 예측 결과와 Label을 이용하여
Cross Entropy Loss를 구해보자

Model_A_pred = np.array([0.05, 0.05, 0.1, 0.15, 0, 0.05, 0.3, 0.1, 0.2, 0])
Model_B_pred = np.array([0.1, 0.1, 0.2, 0, 0.1, 0.2, 0.1, 0.1, 0, 0.1])
Model_C_pred = np.array([0.1, 0.6, 0.2, 0.05, 0, 0, 0.05, 0, 0, 0])
label = np.array([0, 1, 0, 0, 0, 0, 0, 0, 0, 0])def cross_entropy_loss(x):
delta = 1e-7
return -np.sum(label * np.log(x + delta))
print(cross_entropy_loss(Model_A_pred))
print(cross_entropy_loss(Model_B_pred))
print(cross_entropy_loss(Model_C_pred))2.9957302735559908
2.302584092994546
0.510825457099338
가장 정답에 가까운 분포를 가진 Model C가 가장 낮은 loss를 가진다
학습 과정을 반복하며
모델의 출력값과 레이블(정답지)를 비교하며
Cross Entropy Loss를 최소화 하는 방향으로
동시에 Likelihood를 최대화하는 방향으로
학습을 진행한다
PyTorch에서
CrossEntropyLoss()는
LogSoftmax()와 NLLLoss()의 조합
관련 링크
https://gaussian37.github.io/dl-concept-nll_loss/
Softmax와 Negative Log Likelihood Loss 및 Binary Cross Entropy
gaussian37's blog
gaussian37.github.io
출처:
https://huidea.tistory.com/m/276
[Machine learning] 우도(likelihood) 총정리 (MLE, log-likelihood, cross-entropy)
머신러닝을 수식 기반으로 뜯어보면 우도 개념이 빈번히 등장하는데, 우도 개념을 확실히 잡고 가보려한다. 우도는 분류 문제의 loss function 으로 Maximum log-likelihood (MLE)로 등장한다. 우도를 이해
huidea.tistory.com
Youtube, AI Holic - Likelihood 쉽게 설명드려요 - 머신러닝, 인공지능을 위한 수학
Youtube, StatQuest with Josh Starmer - StatQuest: Maximum Likelihood
https://jjangjjong.tistory.com/41
확률(probability)과 가능도(likelihood) 그리고 최대우도추정(likelihood maximization)
* 우선 본 글은 유투브 채널StatQuest with Josh Starmer 님의 자료를 한글로 정리한 것 입니다. 만약 영어듣기가 되신다면 아래 링크에서 직접 보시는 것을 추천드립니다. 이렇게 깔끔하게 설명한 자료
jjangjjong.tistory.com
'Math & Statistics' 카테고리의 다른 글
| Markov Chains, 마르코프 체인 (0) | 2022.05.21 |
|---|---|
| Taylor series, 테일러 급수 (0) | 2022.05.13 |
| 확률과 통계 개념정리 (0) | 2022.03.12 |
| 혼동행렬 - 정확도, 정밀도, 재현율(=민감도), F1 Score (0) | 2022.01.28 |
| Essence of linear algebra 선형대수학 (0) | 2021.12.02 |