오직 세가지 음식(햄버거🍔, 피자🍕, 핫도그🌭)만을 취급하는 레스토랑이 있다고 가정해보자
이 레스토랑에는 특이한 규칙이 하나 있는데 하루에 단 하나의 음식만을 판매한다는 것이다
그리고 그날 어떤 음식을 판매할지는 그 바로 전날 어떤 음식을 팔았느냐에 달려있다

위와 같이 다이어그램으로 표시하면 화살표가 Current State(🍔)에서 Future State(🍕)를 향하고 있다
이는 오늘 햄버거🍔를 팔았을 때 내일 피자🍕를 팔 확률이 60% 라는 뜻이다

위 다이어그램은 가능한 모든 케이스를 나타낸 것이고, 이것이 하나의 마르코프 체인이라고 할 수 있다
Property of Markov Chains, 마르코프 체인의 성질
첫번째 성질
마르코프 체인의 가장 중요한 성질은
미래의 State는 오직 현재의 State에 의존한다 (과거는 고려하지 않는다)
$$ P(X_{n+1} = x | X_{n} = x_{n}) $$
위 다이어그램에 기반하여,
Q. 5월 1일에 🍕, 2일에 🍔, 3일에 🍕를 팔았었다면, 4일에 🌭를 팔 확률은?
↓ 정답 확인
A. 1일에 🍕, 2일에 🍔를 판 것은 아무 상관이 없고,
바로 전날인 3일에 🍕를 팔고, 다음날인 4일에 🌭를 팔 확률만을 보면되기 때문에 답은 70%
두번째 성질
마르코프 체인의 두번째 성질은
다른 State를 향하는 화살표값의 합은 1이다 (확률이기 때문에)
오늘 🍔를 팔았을 때,
내일 🍔를 다시 팔 확률은 20% / 내일 🍕를 팔 확률은 60% / 내일 🌭를 팔 확률은 20%
Stationary distribution
또 다시 예시를 들어보자
🍔 → 🍕 → 🍔 → 🌭 → 🍔 → 🌭 → 🌭 → 🌭 → 🍔 → 🍕
위와 같이 음식을 팔았었다고 한다면 (총 10번의 step)
이제, 각 음식에 대응되는 확률(probability distribution of the states)을 구하길 원한다
이는 간단하게 음식이 등장한 횟수를 전체 일 수로 나눠주면 된다
P(🍔)$= \frac{4}{10}$, P(🍕)$= \frac{2}{10}$, P(🌭)$= \frac{4}{10}$
만약 우리가 step수를 바꾸면, 이 확률값도 변할 것이다
하지만 우리가 진짜 원하는 것은 충분히 오랜 시간동안 지켜봤을때, 이 확률값들이 어떻게 될지가 궁금한 것!
첫번째 접근법: 프로그래밍을 이용한 반복
위에서 그려놓은 다이어그램의 확률을 기반으로 100,000 step의 시뮬레이션 해봤을 때, 다음과 같은 값이 나옴:
P(🍔)$= 0.35191$, P(🍕)$= 0.21245$, P(🌭)$= 0.43564$
충분히 반복해보니, 위와 같이 각 확률이 특정한 값에 수렴(converge)하는 것을 확인할 수 있었다!
이 확률분포(probability distribution)의 특별한 이름이 바로 Stationary distribution 또는 Equilibrium state
이는 위의 확률분포가 이 마르코프 체인(다이어그램)에 대해 시간에 따라 변하지 않음을 의미한다
두번째 접근법: 선형대수학 활용
매번 위와 같이 프로그래밍으로 시뮬레이션 하는 것은 비효율적!
그래서 이 Stationary distribution을 구하기 위한 다른 접근법: 선형대수학 활용
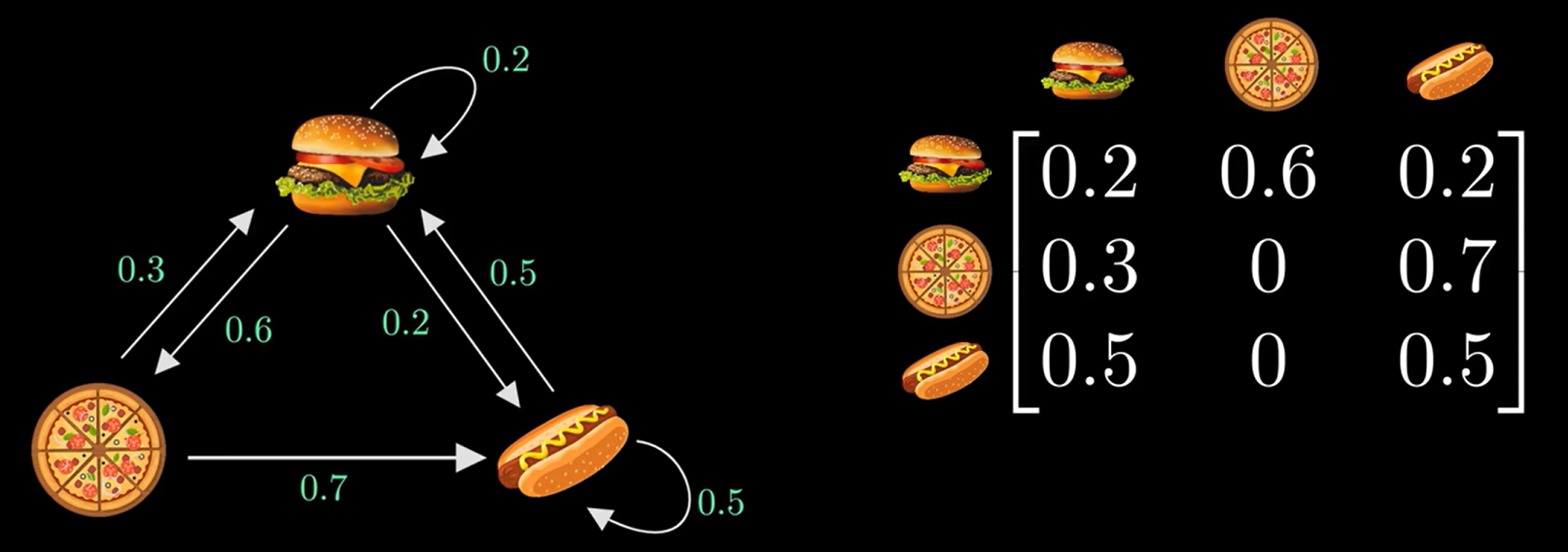
위와 같이 마르코프 체인을 인접행렬로 표시할 수 있다
두번째 행과 첫번째 열이 만나는 지점이 0.3인데
이는 오늘 🍕를 팔았을 때, 내일 🍔를 팔 확률이 30% 라는 의미이다
이는 🍕에서 🍔가 될 전이확률(transition probability)이라고 볼 수 있다 (transition: a에서 b로 향하는 느낌)
그리고 이 행렬을 전이행렬(transition matrix)이라고 부른다
우리의 목표? 각 state의 확률을 찾는 것
위의 전이행렬을 $A$라고 하고
통상적으로 $\pi$로 표시하는 행벡터는 state의 확률을 표현하는 element를 갖고 있음 (즉, state의 확률분포)
이게 무슨소리냐?
오늘이 🍕를 파는 날이라면 $ \pi = [\ 0\ 1\ 0\ ]\quad $ (🍔, 🍕, 🌭 순서)
이 $\pi$를 전이행렬 $A$와 곱하면 🍕에 해당하는 행만이 선택될 것!

$ \pi \times A $의 의미? 오늘 🍕를 팔았을 때, 내일 🍔,🍕,🌭를 팔 각각의 확률을 구하는 것
즉, 현재의 🍕 state에 대응되는 미래의 확률을 얻은 것
구한 결과에 다시 전이행렬을 곱해주면

다시 또 구한 결과에 다시 전이행렬을 곱해주면

만약 stationary state가 존재한다면, 수많은 반복 끝에 출력벡터는 입력벡터와 같아질 것이다
이 특별한 행벡터를 $\pi$라고 하자
이를 수식으로 다시 쓰면
$$ \pi A = \pi $$
이는 선형대수학에서 나오는 고유값에 대한 식과 같다
$$ Av = \lambda v $$
$\lambda = 1$이라고 하고 $A$와 $v$의 곱하는 순서를 바꿔주면 같은 식이 된다
$\pi$를 행렬 $A$의 왼쪽 고유벡터로 생각하고, 고유값은 1이라고 생각할 수 있다
그리고 또 하나의 조건을 만족해야한다
$\pi$의 element들은 합쳐서 1이어야 한다 ($\pi$는 확률분포를 나타내는 것이기 때문에)
$$ \pi [1] + \pi [2] + \pi [3] = 1 $$
결과적으로 다음의 두 식을 풀면
$$ \pi A = \pi $$
$$ \pi [1] + \pi [2] + \pi [3] = 1 $$
계산식
$ \pi = [\ x\quad y\quad z\ ] $ 라고 한다면,
- 첫번째 식 $ \pi A = \pi $ 으로부터
$$ 0.2x + 0.3y + 0.5z = x $$
$$ 0.6x = y $$
$$ 0.2x + 0.7y + 0.5z = z $$
- 두번째 식 $ \pi [1] + \pi [2] + \pi [3] = 1 $ 으로부터
$$ x + y + z = 1 $$
연립방정식을 이용하여 계산
다음과 같은 stationary state를 구할 수 있다
$$ \pi = [\ \frac{25}{71}\quad \frac{15}{71}\quad \frac{31}{71}\ ] $$
$$ \pi = [\ 0.35211\quad 0.21127\quad 0.43662\ ] $$
이를 프로그래밍을 이용한 첫번째 접근법의 결과와 비교해보면
$$ \pi = [\ 0.35191\quad 0.21245\quad 0.43564\ ] $$
결과가 거의 유사함을 알 수 있다
출처: Youtube, Normalized Nerd - Markov Chains Clearly Explained! Part - 1
'Math & Statistics' 카테고리의 다른 글
| 코사인 유사도 (Cosine Similarity) (0) | 2022.06.24 |
|---|---|
| Bayes' theorem 베이즈 정리 (0) | 2022.06.07 |
| Taylor series, 테일러 급수 (0) | 2022.05.13 |
| 확률과 통계 개념정리 (0) | 2022.03.12 |
| Likelihood, MLE, Cross Entropy (0) | 2022.03.11 |