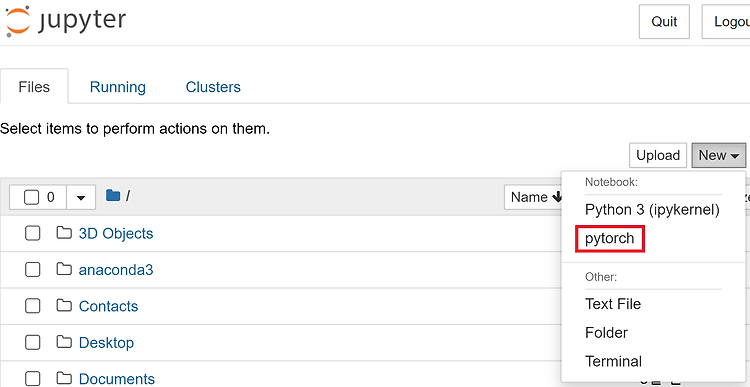
Jupyter Notebook 가상환경 연결
·
Programming/Python
기본적으로 파이썬 패키지들 간의 충돌이 발생할 수 있기 때문에 가상환경으로 분리하여 사용하는 것이 좋다 ! 가상환경을 주피터 노트북에서 사용할 때 다음과 같은 설정이 필요하다 ! Anaconda Prompt 실행 가상환경 생성 및 활성화 conda create -n [가상환경이름] python=[버전] conda activate [가상환경이름] Jupyter 설치 pip install jupyter jupyter notebook과 ipykernel을 따로 설치해도 되지만, 위의 한줄로 해결 가능하다! 커널 연결 python -m ipykernel install --user --name [가상환경이름] --display-name [설정할커널이름] Jupyter Notebook 실행 jupyter noteb..

