머신러닝의 Logistic Regression
딥러닝의 Softmax function
과도 관련이 있는 "Logit"을 알아보기 위해
Odds라는 개념도 알아보자!
(통계학에서 나온 개념들)
Odds, 오즈
8번의 경기가 치뤄졌는데 그 중 5번 이기고, 3번 졌다면
$$ odds = \frac{5}{3} = 1.667 $$

유의할 점으로 오즈는 확률이 아니다!!
$$ odds \ne probability $$

odds는 단순히 횟수(counts)로도 구할 수 있고, 확률(probability)로도 구할 수 있음
$$ odds = \frac{5}{3} = \frac{\frac{5}{8}}{\frac{3}{8}} = \frac{p}{1-p} $$
하지만 odds는 크나큰 단점이 존재하는데!
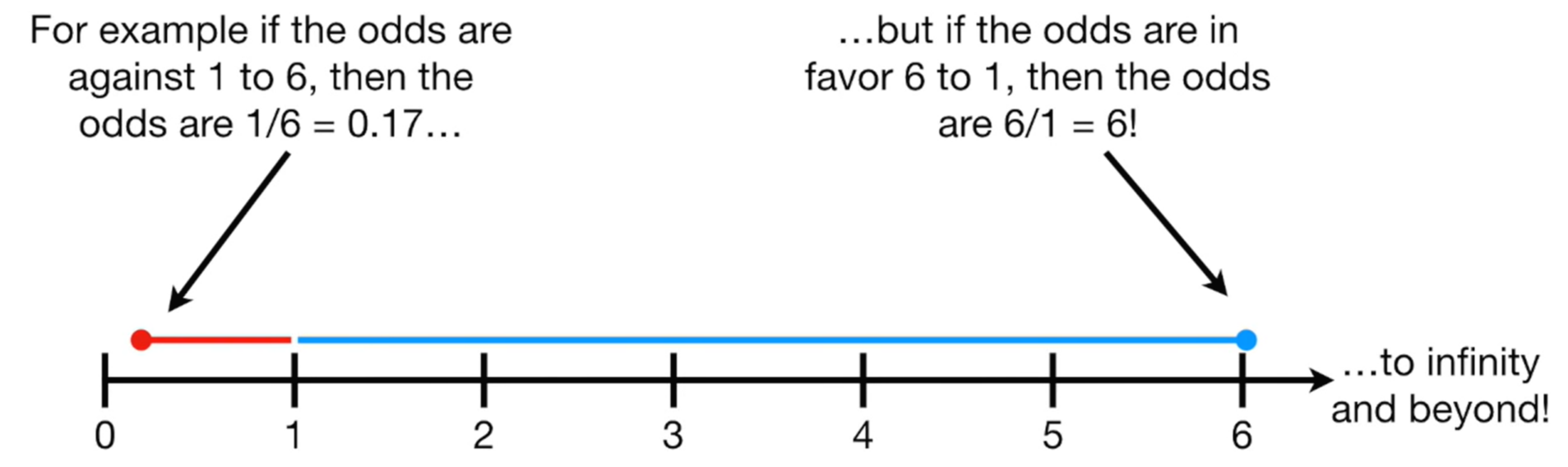
만약 1번 승리하고 6번 패배했다면, $odds = \frac{1}{6} = 0.1667$
만약 6번 승리하고 1번 패배했다면, $odds = \frac{6}{1} = 6$
더 극단적으로 생각해보면
만약 1번 승리하고 12345번 패배했다면, $odds = \frac{1}{12345} = 0.000081$
만약 12345번 승리하고 1번 패배했다면, $odds = \frac{12345}{1} = 12345$
즉, 승리횟수가 패배횟수보다 적을 경우, odds는 $0 \sim 1$사이의 값을 가지지만
반대로 승리횟수가 패배횟수보다 많을 경우, odds는 $1 \sim \infty$의 값을 가짐
이러한 비대칭성은 비교를 어렵게 만든다!
그래서 로그(log)를 적용하여 대칭적으로 만듦

만약 1번 승리하고 6번 패배했다면, $log(odds) = log(\frac{1}{6}) = -1.792$
만약 6번 승리하고 1번 패배했다면, $log(odds) = log(\frac{6}{1}) = 1.792$
이렇게 로그를 취해주면 전과는 다르게 양쪽의 거리가 같다!
Logit, 로짓
위에서 odds를 구할 때, 횟수로도 구하고 확률로도 구할 수 있었다!
$$ odds = \frac{5}{3} = \frac{\frac{5}{8}}{\frac{3}{8}} = \frac{p}{1-p} $$
이에 로그를 취해주면
$$ log(odds) = \log(\frac{5}{3}) = log(\frac{\frac{5}{8}}{\frac{3}{8}}) = log(\frac{p}{1-p}) $$
Logit : odds에 log를 취해준 것, $ Logit = log(\frac{p}{1-p}) $
odds의 단점을 log를 취해 극복한 것이 바로 logit!
딥러닝에서 Multi-class Classification 문제를 풀 때
Input layer, Hidden layer를 지나서
Output layer의 Softmax function을 지나기 전의 값들이 Logit !
이 Logit들이 Softmax function을 지나서 확률이 된다
출처 : Youtube, StatQuest with Josh Starmer - Odds and Log(Odds), Clearly Explained!!!
'Programming > DL, Deep Learning' 카테고리의 다른 글
| Epoch, Batch size, Step, Iteration (1) | 2023.01.17 |
|---|---|
| PyTorch (2) | 2023.01.11 |
| Logit, Sigmoid, Softmax (0) | 2022.05.14 |
| PyTorch Tutorial (0) | 2022.02.15 |